streamalism.org

1. Bemutatkozás

Ennek a sorozatnak a célja a genetikai algoritmusok ötletének ismertetése és a legismertebb megvalósítások bemutatása.

Ebben az oktatóanyagban megtesszük írjon le egy nagyon hatékony Jenetics Java könyvtárat, amely különféle optimalizálási problémák megoldására használható.

Ha úgy érzi, hogy többet kell megtudnia a genetikai algoritmusokról, javasoljuk, hogy ezzel a cikkel kezdje.

2. Hogyan működik?

Hivatalos dokumentumai szerint a Jenetics egy Java-ban írt evolúciós algoritmuson alapuló könyvtár. Az evolúciós algoritmusok a biológiában gyökereznek, mivel olyan mechanizmusokat alkalmaznak, amelyeket a biológiai evolúció inspirált, például reprodukció, mutáció, rekombináció és szelekció.

A Jenetics a Java segítségével valósul meg Folyam interfész, így simán működik a többi Java-val Folyam API.

A főbb jellemzők:

• súrlódás nélküli minimalizálás - nincs szükség a fitnesz funkció megváltoztatására vagy módosítására; csak megváltoztathatjuk a Motor osztály és készen állunk az első jelentkezés megkezdésére
• függőségtől mentes - nincsenek futásidejű, harmadik féltől származó könyvtárak a Jenetics használatához
• Java 8 készen áll - teljes támogatás a Folyam és lambda kifejezések
• többszálú - az evolúciós lépések párhuzamosan végrehajthatók

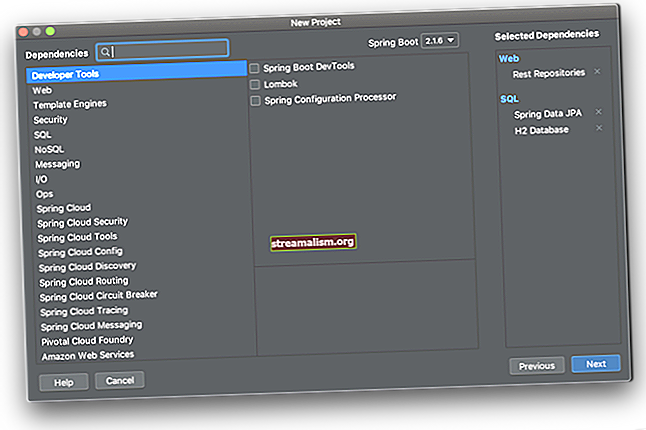
A Jenetics használatához a következő függőséget kell hozzáadnunk pom.xml:

 io.jenetics jenetics 3.7.0 

A legújabb verzió a Maven Central oldalon található.

3. Használjon tokokat

A Jenetics összes szolgáltatásának teszteléséhez megpróbálunk megoldani különféle jól ismert optimalizálási problémákat, kezdve az egyszerű bináris algoritmustól és a Knapsack problémáig.

3.1. Egyszerű genetikai algoritmus

Tegyük fel, hogy meg kell oldanunk a legegyszerűbb bináris problémát, ahol optimalizálnunk kell az 1 bit pozícióit a 0-ból és 1-ből álló kromoszómában. Először meg kell határoznunk a problémára alkalmas gyárat:

Gyár gtf = genotípus (bit (10, 0,5) kromoszóma);

Mi hoztuk létre a BitChromosoma 10 hosszúságú, és annak valószínűsége, hogy a kromoszómában 1 legyen 0,5,

Most hozzuk létre a végrehajtási környezetet:

Motor motor = Motor.builder (SimpleGeneticAlgorithm :: eval, gtf) .build ();

A eval () metódus adja vissza a bitszámot:

private Integer eval (genotípus gt) {return gt.getChromosome (). as (BitChromosome.class) .bitCount (); }

Az utolsó lépésben elindítjuk az evolúciót és összegyűjtjük az eredményeket:

Genotípus eredménye = motor.stream () .limit (500) .collect (EvolutionResult.toBestGenotype ());

A végeredmény hasonló lesz ehhez:

Az evolúció előtt: [00000010 | 11111100] Az evolúció után: [00000000 | 11111111]

Sikerült optimalizálni az 1-ek helyzetét a génben.

3.2. Részhalmazösszeg probléma

A Jenetics másik felhasználási esete a részhalmaz összegének problémájának megoldása. Röviden, az optimalizálás kihívása az, hogy egy egész számhalmaz alapján meg kell találnunk egy nem üres részhalmazt, amelynek összege nulla.

Az ilyen problémák megoldására előre meghatározott interfészek vannak a Jenetics alkalmazásban:

public class A SubsetSum végrehajtja a problémát {// implementáció}

Mint láthatjuk, a Probléma, amelynek három paramétere van:

• - a problémás fitnesz függvény argumentumtípusa, esetünkben megváltoztathatatlan, rendezett, fix méretű Egész szám sorrend ISeq
• - az a géntípus, amellyel az evolúciós motor dolgozik, ebben az esetben megszámlálható Egész szám gének EnumGene
• - a fitnesz funkció eredménytípusa; itt van egy Egész szám

A Probléma felületen felül kell írnunk két módszert:

@Orride public Function fitness () {return részhalmaz -> Math.abs (subset.stream () .mapToInt (Integer :: intValue) .sum ()); } @Orride public Codec kodek () {return codecs.ofSubSet (basicSet, méret); }

Az elsőben meghatározzuk a fitneszfunkciónkat, míg a második egy osztály, amely gyári módszereket tartalmaz a közös problémakódolások létrehozására, például egy adott alapkészletből a legjobb rögzített méretű részhalmaz megtalálására, mint esetünkben.

Most folytathatjuk a fő részt. Az elején létre kell hoznunk egy alcsoportot, amelyet a problémában használhatunk:

SubsetSum probléma = (500, 15, új LCG64ShiftRandom (101010));

Felhívjuk figyelmét, hogy a LCG64ShiftRandom generátort a Jenetics szolgáltatta. A következő lépésben a megoldás motorját építjük:

A következő lépésben a megoldás motorját építjük:

Motor motor = Motor.builder (probléma) .minimalizálva () .maximalPhenotypeAge (5) .alterers (új PartiallyMatchedCrossover (0.4), új Mutator (0.3)) .build ();

Megpróbáljuk minimalizálni az eredményt (optimális esetben az eredmény 0 lesz) azáltal, hogy meghatározzuk a fenotípus korát és az utódok megváltoztatásához használt változtatókat. A következő lépésben megkapjuk az eredményt:

Fenotípus eredmény = motor.stream () .limit (limit.bySteadyFitness (55)) .collect (EvolutionResult.toBestPhenotype ());

Felhívjuk figyelmét, hogy használjuk bySteadyFitness () amely egy predikátumot ad vissza, amely meg fogja csonkolni az evolúciós áramlatot, ha a megadott generációk száma után nem lehet jobb fenotípust találni és a legjobb eredményt gyűjteni. Ha szerencsénk lesz, és van megoldás a véletlenszerűen létrehozott halmazra, ehhez hasonlót fogunk látni:

Ha szerencsénk lesz, és van megoldás a véletlenszerűen létrehozott halmazra, ehhez hasonlót fogunk látni:

[85|-76|178|-197|91|-106|-70|-243|-41|-98|94|-213|139|238|219] --> 0

Ellenkező esetben a részhalmaz összege eltér a 0-tól.

3.3. Hátizsák első illesztési probléma

A Jenetics könyvtár lehetővé teszi számunkra, hogy még kifinomultabb problémákat oldjunk meg, például a Knapsack problémát. Röviden szólva: ebben a problémában korlátozott hely van a hátizsákunkban, és el kell döntenünk, hogy mely elemeket tegyük bele.

Kezdjük a táska méretének és a cikkek számának meghatározásával:

int nTételek = 15; kettős ksSize = nItems * 100,0 / 3,0;

A következő lépésben létrehozunk egy véletlenszerű tömböt, amely tartalmazza KnapsackItem objektumok (által definiált méret és érték mezők), és ezeket az elemeket véletlenszerűen tesszük a hátizsákba, az First Fit módszerrel:

KnapsackFF ff = new KnapsackFF (Stream.generate (KnapsackItem :: random) .limit (nItems) .toArray (KnapsackItem [] :: new), ksSize);

Ezután létre kell hoznunk a Motor:

Motor motor = Engine.builder (ff, BitChromosome.of (nItems, 0.5)) .populationSize (500) .survivorsSelector (new TournamentSelector (5)) .offspringSelector (new RouletteWheelSelector ()) .terterers (new Mutator (0.115), new SinglePointCrossover (0,16)) .építés ();

Néhány megjegyzendő pont itt:

• a népesség nagysága 500 fő
• az utódokat a verseny és a rulett kerék kiválasztásával választják ki
• ahogy az előző alfejezetben tettük, meg kell határoznunk az újonnan létrehozott utódok módosítóit is

A Jeneticsnek van egy nagyon fontos jellemzője is. Könnyen összegyűjthetjük az összes statisztikát és betekintést a szimuláció teljes időtartamára. Ezt a EvolutionStatistics osztály:

EvolutionStatistics statistics = EvolutionStatistics.ofNumber ();

Végül futtassuk a szimulációkat:

Legjobb fenotípus = motor.stream () .limit (bySteadyFitness (7)) .limit (100) .peek (statisztika) .collect (toBestPhenotype ());

Felhívjuk figyelmét, hogy az értékelési statisztikákat minden generáció után frissítjük, amely legfeljebb 7 állandó generációra és összesen legfeljebb 100 generációra korlátozódik. Részletesebben két lehetséges forgatókönyv létezik:

• 7 állandó generációt érünk el, akkor a szimuláció leáll
• 100 generációnál kevesebb 7 generációt nem tudunk elérni, így a szimuláció a második miatt leáll határ()

Fontos a maximális generációs korlátozás, különben előfordulhat, hogy a szimulációk ésszerű időn belül nem állnak le.

A végeredmény sok információt tartalmaz:

+ ------------------------------------------------- -------------------------- + | Idő statisztika | + ------------------------------------------------- -------------------------- + | Kiválasztás: összeg = 0,039207931000 s; átlag = 0,003267327583 s | | Változás: összeg = 0,065145069000 s; átlag = 0,005428755750 s | | Fitneszszámítás: összeg = 0,029678433000 s; átlag = 0,002473202750 s | | Teljes végrehajtás: összeg = 0,111383965000 s; átlag = 0,009281997083 s | + ------------------------------------------------- -------------------------- + | Fejlődési statisztika | + ------------------------------------------------- -------------------------- + | Generációk: 12 | | Módosítva: összeg = 7 664; átlag = 638,666666667 | | Megölt: összeg = 0; átlag = 0,000000000 | | Érvénytelen: összeg = 0; átlag = 0,000000000 | + ------------------------------------------------- -------------------------- + | Népességi statisztika + ------------------------------------------------- -------------------------- + | Kor: max = 10; átlag = 1,792167; var = 4,657748 | | Fitnesz: | | min = 0,000000000000 | | max = 716,684883338605 | | átlag = 587,012666759785 | | var = 17309,892287851708 | | std = 131,567063841418 | + ------------------------------------------------- -------------------------- +

Ebben a pillanatban 716,68 összértékű elemeket tudtunk elhelyezni a legjobb forgatókönyv szerint. Láthatjuk az evolúció és az idő részletes statisztikáit is.

Hogyan kell tesztelni?

Ez egy meglehetősen egyszerű folyamat - csak nyissa meg a problémához kapcsolódó fő fájlt, és először futtassa az algoritmust. Ha van egy általános elképzelésünk, akkor elkezdhetünk játszani a paraméterekkel.

4. Következtetés

Ebben a cikkben a Jenetics könyvtár szolgáltatásait ismertettük valós optimalizálási problémák alapján.

A kód Maven projektként érhető el a GitHubon. Felhívjuk figyelmét, hogy a kód példákat adtunk további optimalizálási kihívásokhoz, például a Springsteen Record (igen, létezik!) És a Traveling Salesman problémákhoz.

Nézze meg a következő linkeket a sorozat összes cikkéhez, beleértve a genetikai algoritmusok egyéb példáit is:

• Hogyan lehet genetikai algoritmust megtervezni a Java-ban
• Az utazó eladó problémája a Java-ban
• Hangya telep optimalizálása
• Bevezetés a Jenetics könyvtárba (ez)