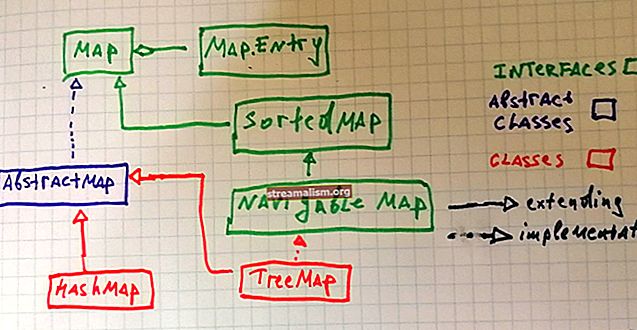
Gyakorlati Java példák a nagy O jelölésre
1. Áttekintés
Ebben az oktatóanyagban arról fogunk beszélni, hogy mi A Big O jelölés azt jelenti. Néhány példát mutatunk be, hogy megvizsgáljuk a kód futási idejére gyakorolt hatását.
2. A nagy O jelölés intuíciója
Gyakran halljuk a a Big O Notation segítségével leírt algoritmus teljesítménye.
Az algoritmusok - vagy algoritmikus komplexitás - teljesítményének vizsgálata az algoritmuselemzés területére esik. Az algoritmuselemzés arra a kérdésre ad választ, hogy egy algoritmus hány erőforrást - például lemezterületet vagy időt - használ fel.
Az időt erőforrásként fogjuk vizsgálni. Általában minél kevesebb idő telik el egy algoritmus elkészítéséhez, annál jobb.
3. Állandó idejű algoritmusok - O (1)
Hogyan befolyásolja az algoritmus ez a bemeneti mérete a futási idejét? A Big O megértésének kulcsa a dolgok növekedési sebességének megértése. A kérdéses arány itt bemeneti méretenként vett idő.
Fontolja meg ezt az egyszerű kóddarabot:
int n = 1000; System.out.println ("Hé - a bemenet:" + n);Egyértelmű, hogy nem mindegy, mi n felül van. Ennek a kódrésznek a futtatása állandó ideig tart. Ez nem függ az n méretétől.
Hasonlóképpen:
int n = 1000; System.out.println ("Hé - a bemenet:" + n); System.out.println ("Hmm .. Több dolgot csinálok a következővel:" + n); System.out.println ("És még sok más:" + n);A fenti példa szintén állandó idő. Még akkor is, ha háromszor annyi időbe telik a futás nem függ a bemenet méretétől, n. Az állandó idejű algoritmusokat a következőképpen jelöljük: O (1). Vegye figyelembe, hogy O (2), O (3) vagy akár O (1000) ugyanazt jelentené.
Nem érdekel, hogy pontosan mennyi idő alatt futunk, csak az, hogy állandó időbe telik.
4. Logaritmikus idő algoritmusok - O (log n)
Az állandó idejű algoritmusok (aszimptotikusan) a leggyorsabbak. A logaritmikus idő a következő leggyorsabb. Sajnos kissé trükkösebbek elképzelni őket.
A logaritmikus időalgoritmus egyik gyakori példája a bináris keresési algoritmus. Kattintson ide a bináris keresés Java-ban történő megvalósításának megtekintéséhez.
Ami itt fontos, hogy a a futási idő arányosan növekszik a bemenet logaritmusával (ebben az esetben jelentkezzen be a 2. bázisra):
for (int i = 1; i <n; i = i * 2) {System.out.println ("Hé - elfoglalt vagyok, ha ránézek:" + i); }Ha n értéke 8, a kimenet a következő lesz:
Hé - elfoglalt a nézés: 1 Hé - elfoglalt a nézés: 2 hé - elfoglalt a nézés: 4Egyszerű algoritmusunk log (8) = 3-szor futott.
5. Lineáris idő algoritmusok - Tovább)
A logaritmikus időalgoritmusok után megkapjuk a következő leggyorsabb osztályt: lineáris idő algoritmusok.
Ha azt mondjuk, hogy valami lineárisan növekszik, akkor azt értjük, hogy közvetlenül arányos a bemeneteinek méretével.
Gondolj egy egyszerű ciklusra:
for (int i = 0; i <n; i ++) {System.out.println ("Hé - elfoglalt vagyok, ha ránézek:" + i); }Hányszor fut ez a huroknál? n természetesen, természetesen! Nem tudjuk pontosan, hogy ez mennyi időbe telik, és ez nem aggódik.
Amit tudunk, az az, hogy a fent bemutatott egyszerű algoritmus lineárisan növekszik a bemenet nagyságával.
Jobban szeretnénk egy futási időt 0,1n mint (1000n + 1000), de mindkettő továbbra is lineáris algoritmus; mindkettő közvetlenül nő a ráfordítások méretével arányosan.
Ismételten, ha az algoritmust a következőkre változtattuk:
for (int i = 0; i <n; i ++) {System.out.println ("Hé - elfoglalt vagyok, ha ránézek:" + i); System.out.println ("Hmm .. Nézzük meg még egyszer:" + i); System.out.println ("És még egy:" + i); }A futásideje továbbra is lineáris lenne a bemeneti méretben, n. A lineáris algoritmusokat a következőképpen jelöljük: Tovább).
Csakúgy, mint a konstans idejű algoritmusok esetében, itt sem törődünk a futási idő sajátosságaival. O (2n + 1) ugyanaz mint Tovább), mivel a Big O Notation a bemeneti méret növekedésével foglalkozik.
6. N Log N idő algoritmusok - O (n log n)
n log n az algoritmusok következő osztálya. A futási idő arányosan nő n log n a bemenet
for (int i = 1; i <= n; i ++) {for (int j = 1; j <n; j = j * 2) {System.out.println ("Hé, elfoglalt vagyok, ha megnézem:" + i + "és" + j); }} Például, ha a n értéke 8, akkor ez az algoritmus futni fog 8 * log (8) = 8 * 3 = 24 alkalommal. Az, hogy szigorú egyenlőtlenségünk van-e vagy sem a for ciklusban, a Big O jelölés szempontjából lényegtelen.
7. Polinomiális idő algoritmusok - O (np)
Ezután polinomiális idő algoritmusokat kapunk. Ezek az algoritmusok még lassabbak, mint n log n algoritmusok.
A polinom kifejezés általános kifejezés, amely másodfokú (n2), köbös (n3), kvartikus (n4)stb funkciók. Amit fontos tudni, az az O (n2) gyorsabb, mint O (n3) ami gyorsabb, mint O (n4)stb.
Vessünk egy pillantást a másodfokú idő algoritmus egyszerű példájára:
for (int i = 1; i <= n; i ++) {for (int j = 1; j <= n; j ++) {System.out.println ("Hé - elfoglalt a nézés:" + i + "és" + j); }} Ez az algoritmus futni fog 82 = 64 alkalommal. Megjegyezzük, hogy ha egy másikat fészkelnénk a hurokhoz, akkor ez egy O (n3) algoritmus.
8. Exponenciális idő algoritmusok - O (kn)
Most veszélyes területre kerülünk; ezek az algoritmusok a bemeneti méret által hatványozott tényezővel arányosan nőnek.
Például, O (2n) az algoritmusok minden további bemenettel megduplázódnak. Tehát, ha n = 2, ezek az algoritmusok négyszer fognak futni; ha n = 3, nyolcszor fognak futni (olyan, mint a logaritmikus időalgoritmusok ellentéte).
O (3n) algoritmusok megháromszorozódnak minden további bemenetnél, O (kn) az algoritmusok minden további bemenet esetén k-szor nagyobbak lesznek.
Vessünk egy pillantást egy egyszerű példára O (2n) idő algoritmus:
for (int i = 1; i <= Math.pow (2, n); i ++) {System.out.println ("Hé - elfoglalt vagyok, ha ránézek:" + i); }Ez az algoritmus futni fog 28 = 256 alkalommal.
9. Faktoriális idő algoritmusok - Tovább!)
A legtöbb esetben ez nagyjából olyan rossz, mint amilyenné válik. Ennek az algoritmusosztálynak a futási ideje arányos a bemeneti méret tényezőjével.
Klasszikus példa erre az utazó eladó problémájának megoldása, egy durva erő megközelítésével annak megoldására.
Az utazó eladó problémájának megoldásának magyarázata meghaladja a cikk kereteit.
Nézzünk inkább egy egyszerűt Tovább!) algoritmus, az előző szakaszokhoz hasonlóan:
mert (int i = 1; i <= faktoriális (n); i ++) {System.out.println ("Hé - elfoglalt vagyok, ha ránézek:" + i); }hol tényező (n) egyszerűen kiszámítja az n-t. Ha n értéke 8, akkor ez az algoritmus futni fog 8! = 40320 alkalommal.
10. Aszimptotikus funkciók
A Big O az úgynevezett an aszimptotikus funkció. Mindez azt jelenti, hogy egy algoritmus teljesítményével foglalkozik a határon - azaz - amikor sok bemenet dobódik rá.
A Big O nem törődik azzal, hogy az algoritmusod milyen jól működik a kis méretű bemenetekkel. Nagy bemenetekkel foglalkozik (gondoljon arra, hogy válogasson egymillió számot, vagy válasszon 5 számot).
Egy másik dolog, amit meg kell jegyezni, az vannak más aszimptotikus funkciók. A Big Θ (theta) és Big Ω (omega) szintén leírja az algoritmusokat a határértéknél (ne feledje, a határ ez csak azt jelenti, hogy hatalmas bemenetekre van szükség).
A 3 fontos funkció közötti különbségek megértéséhez először tudnunk kell, hogy a Big O, a Big Θ és a Big Ω mindegyike leír egy készlet (azaz elemek gyűjteménye).
Itt halmazaink tagjai maguk algoritmusok:
- A nagy O az összes futó algoritmus halmazát írja le nem rosszabb mint egy bizonyos sebesség (ez egy felső határ)
- Ezzel szemben a Big Ω leírja az összes futó algoritmus halmazát nem jobb mint egy bizonyos sebesség (ez egy alsó határ)
- Végül Big Θ leírja az összes futó algoritmus halmazát nál nél egy bizonyos sebesség (olyan, mint az egyenlőség)
A fenti fogalommeghatározások matematikailag nem pontosak, de segítenek megértésünkben.
Általában a Big O segítségével leírt dolgokat hallja, de nem árt tudni a Big Θ-ról és a Big Ω-ról.
11. Következtetés
Ebben a cikkben megvitattuk a Big O jelölést és hogyan Az algoritmus bonyolultságának megértése befolyásolhatja a kód futási idejét.
A különböző bonyolultsági osztályok nagyszerű megjelenítését itt találja.
Szokás szerint ennek az oktatóanyagnak a kódrészletei megtalálhatók a GitHubon.