streamalism.org

1. Áttekintés

Az algoritmusok futásidejű bonyolultsága gyakran függ a bemenet jellegétől.

Ebben az oktatóanyagban meglátjuk, hogyan a Quicksort algoritmus triviális megvalósítása gyenge teljesítményt mutat az ismételt elemek számára.

Megtanulunk néhány Quicksort-változatot a bemenetek hatékony particionálásához és rendezéséhez nagy sűrűségű duplikált kulcsokkal.

2. Triviális Quicksort

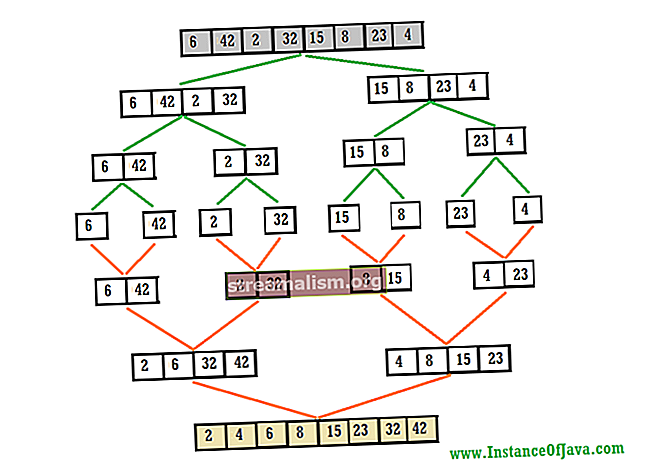
A Quicksort egy hatékony rendezési algoritmus, amely a divide and conquer paradigmán alapul. Funkcionálisan szólva a helyén működik a bemeneti tömbön, és egyszerű összehasonlítással és csere műveletekkel átrendezi az elemeket.

2.1. Egycsuklós particionálás

A Quicksort algoritmus triviális megvalósítása nagymértékben támaszkodik az egycsuklós particionálási eljárásra. Más szavakkal, a particionálás elosztja az A = [a_o, a_{p + 1}, a_{p + 2},…, A_r] két részre A [p..q] és A [q + 1..r] úgy, hogy:

• Az összes elem az első partícióban, A [p..q] kisebb vagy egyenlő az A [q] forgási értékkel
• A második partíció összes eleme, A [q + 1..r] nagyobb vagy egyenlő az A [q] forgási értékkel

Ezt követően a két partíciót független bemeneti tömbként kezelik, és betáplálják a Quicksort algoritmusba. Lássuk Lomuto Quicksortját működés közben:

2.2. Teljesítmény ismételt elemekkel

Tegyük fel, hogy van egy A = [4, 4, 4, 4, 4, 4, 4] tömb, amelynek minden eleme egyenlő.

Ha ezt a tömböt az egycsuklós particionálási sémával particionáljuk, két partíciót kapunk. Az első partíció üres lesz, míg a második partíció N-1 elemeket tartalmaz. További, a partíciós eljárás minden további meghívása csak egyrel csökkenti a bemeneti méretet. Nézzük meg, hogyan működik:

Mivel a partíciós eljárás lineáris időbonyolultságú, az idő időbeli összetettsége ebben az esetben kvadratikus. Ez a legrosszabb forgatókönyv bemeneti tömbünkhöz.

3. Háromirányú felosztás

A nagy számú ismételt kulcsot tartalmazó tömb hatékony rendezéséhez választhatunk, hogy az egyenlő kulcsokat felelősségteljesebben kezeljük. Az ötlet az, hogy megfelelő helyzetbe hozzuk őket, amikor először találkozunk velük. Tehát, amit keresünk, a tömb három partíciós állapota:

• A bal oldali partíció olyan elemeket tartalmaz, amelyek szigorúan kisebbek, mint a particionálási kulcs
• AA középső partíció minden elemet tartalmaz, amely megegyezik a partíciós kulccsal
• A jobb oldali partíció minden olyan elemet tartalmaz, amely szigorúan nagyobb, mint a particionálási kulcs

Most mélyebben belemerülünk néhány olyan megközelítésbe, amelyekkel háromirányú particionálást érhetünk el.

4. Dijkstra megközelítése

Dijkstra megközelítése a háromirányú felosztás hatékony módja. Ennek megértéséhez nézzünk meg egy klasszikus programozási problémát.

4.1. Holland nemzeti lobogó probléma

A holland trikolor zászló inspirálta Edsger Dijkstra programozási problémát javasolt a Holland Nemzeti Zászló Probléma (DNF) néven.

Dióhéjban az átrendeződési probléma, ahol véletlenszerűen egy vonalba helyezett három színű golyót kapunk, és arra kérnek bennünket, hogy ugyanazokat a színes golyókat csoportosítsák össze. Ezenkívül az átrendezésnek biztosítania kell, hogy a csoportok a helyes sorrendet kövessék.

Érdekes, hogy a DNF probléma szembetűnő analógiát mutat egy ismételt elemeket tartalmazó tömb háromirányú felosztásával.

Egy tömb összes számát három csoportba sorolhatjuk egy adott kulcs szempontjából:

• A Piros csoport minden olyan elemet tartalmaz, amely szigorúan kisebb, mint a kulcs
• A Fehér csoport minden elemet tartalmaz, amely megegyezik a kulccsal
• A Kék csoport minden olyan elemet tartalmaz, amely szigorúan nagyobb, mint a kulcs

4.2. Algoritmus

A DNF probléma megoldásának egyik megközelítése az, hogy az első elemet választja partíciós kulcsnak, és a tömböt balról jobbra vizsgálja. Az egyes elemek ellenőrzése során a megfelelő csoportba helyezzük, nevezetesen a Lesser, az Equal és a Greater csoportokba.

A particionálás előrehaladásának nyomon követéséhez három mutató segítségére lenne szükségünk, nevezetesen lt, jelenlegi, és gt. Az idő bármely pontján a bal oldali elemek lt szigorúan kisebb lesz, mint a particionálási kulcs, és a tőlük jobbra levő elemek gt szigorúan nagyobb lesz, mint a kulcs.

Továbbá használjuk a jelenlegi mutató a beolvasáshoz, ami azt jelenti, hogy a jelenlegi és gt a mutatókat még fel kell tárni:

Először is beállíthatjuk lt és jelenlegi mutatók a tömb legelején és a gt mutató a legvégén:

Minden elemen keresztül olvasható a jelenlegi mutató, összehasonlítjuk a particionáló kulccsal, és elvégezzük a három összetett művelet egyikét:

• Ha bemenet [aktuális] <gomb, akkor cserélünk bemenet [áram] és bemenet [lt] és növekszik mindkettő jelenlegi és lt mutatók
• Ha bemenet [áram] == kulcs, akkor növekszünk jelenlegi mutató
• Ha input [current]> gomb, akkor cserélünk bemenet [áram] és bemenet [gt] és csökkentés gt

Végül is, megállunk, amikor a jelenlegi és gt mutatók keresztezik egymást. Ezzel a feltáratlan régió mérete nullára csökken, és csak három szükséges partíció marad.

Végül nézzük meg, hogyan működik ez az algoritmus egy bemeneti tömbön, amelynek duplikált elemei vannak:

4.3. Végrehajtás

Először írjunk egy segédprogram eljárást összehasonlít () háromszámú összehasonlítást végezni két szám között:

public static int összehasonlítás (int szám1, int szám2) {if (szám1> szám2) 1-es visszatérés; else if (num1 <num2) return -1; else visszatér 0; }

Ezután adjunk hozzá egy úgynevezett metódust csere() elemeket cserélni ugyanazon tömb két indexén:

public static void swap (int [] tömb, int helyzet1, int helyzet2) {if (helyzet1! = helyzet2) {int temp = tömb [helyzet1]; tömb [helyzet1] = tömb [helyzet2]; tömb [helyzet2] = hőmérséklet; }}

A partíció egyedi azonosításához a tömbben szükségünk lesz a bal és a jobb határindexekre. Tehát folytassuk és hozzunk létre egy Partíció osztály:

public class Partíció {private int left; magán int jog; }

Most készen állunk a háromirányú írásunkra partíció () eljárás:

public static Partíció partíció (int [] bemenet, int kezdet, int vég) {int lt = kezdet, aktuális = kezdet, gt = vég; int partitioningValue = input [kezdet]; while (current <= gt) {int CompareCurrent = összehasonlítás (input [current], partitioningValue); kapcsoló (CompareCurrent) {eset -1: csere (bemenet, áram ++, lt ++); szünet; 0. eset: áram ++; szünet; 1. eset: csere (bemenet, áram, gt--); szünet; }} return new partition (lt, gt); }

Végül írjunk egy quicksort () módszer, amely a 3-utas particionálási sémánkat használja a bal és a jobb partíció rekurzív rendezéséhez:

public static void quicksort (int [] input, int begin, int end) {if (end <= begin) return; Partition middlePartition = partíció (bemenet, kezdet, vég); quicksort (input, begin, middlePartition.getLeft () - 1); quicksort (input, middlePartition.getRight () + 1, end); }

5. Bentley-McIlroy megközelítése

Jon Bentley és Douglas McIlroy társszerzője egy a Quicksort algoritmus optimalizált változata. Értsük meg és valósítsuk meg ezt a változatot a Java-ban:

5.1. Particionálási séma

Az algoritmus lényege egy iteráció alapú particionálási séma. Kezdetben a teljes számtömb számunkra feltáratlan terület:

Ezután elkezdjük felfedezni a tömb elemeit bal és jobb irányból. Amikor belépünk vagy elhagyjuk a kutatási kört, öt tömb összetételeként jeleníthetjük meg a tömböt:

• A két legvégén azok a régiók találhatók, amelyeknek elemei megegyeznek a particionálási értékkel
• A feltáratlan régió a középpontban marad, és mérete minden egyes iterációnál folyamatosan csökken
• A feltáratlan régió bal oldalán található minden elem, amely kisebb, mint a particionálási érték
• A feltáratlan régió jobb oldalán a partíciós értéknél nagyobb elemek találhatók

Végül a feltárási ciklusunk akkor szűnik meg, amikor már nincsenek elemezhető elemek. Ebben a szakaszban a a feltáratlan régió mérete gyakorlatilag nulla, és csak négy régiónk marad:

Ezután mi mozgassa az összes elemet a középen lévő két egyenlő régióból úgy, hogy csak egy egyenlő terület legyen a közepén, amelyet a bal oldali kevesebb, a jobb pedig a nagyobb régió vesz körül. Ehhez először a bal egyenlő régióban lévő elemeket cseréljük fel a kevésbé régió jobb végén lévő elemekkel. Hasonlóképpen, a jobb egyenlő régióban lévő elemeket felcseréljük a nagyobb régió bal végén lévő elemekkel.

Végül mi leszünk csak három partícióval maradt, és tovább használhatjuk ugyanazt a megközelítést a kisebb és nagyobb régiók felosztásához.

5.2. Végrehajtás

A háromutas Quicksort rekurzív megvalósításakor meg kell hívnunk a partíciós eljárást olyan résztömbök esetében, amelyeknek különböző alsó és felső határai vannak. Szóval, a mi partíció () A metódusnak három bemenetet kell elfogadnia, nevezetesen a tömböt a bal és jobb oldali határaival együtt.

public static Partíció partíció (int bemenet [], int kezdet, int vég) {// a partíció ablakát adja vissza}

Az egyszerűség kedvéért megtehetjük válassza a particionálási értéket a tömb utolsó elemeként. Adjunk meg két változót is balra = kezd és jobb = vég hogy felfedezzék a tömböt befelé.

Továbbá nekünk is meg kell kövesse nyomon a bal és a jobb szélen fekvő egyenlő elemek számát. Tehát kezdjük leftEqualKeysCount = 0 és rightEqualKeysCount = 0, és most már készen állunk a tömb feltárására és felosztására.

Először elkezdünk mozogni mindkét irányból és inverziót találni ahol a bal oldalon lévő elem nem kisebb, mint a particionálási érték, és a jobb oldali elem nem nagyobb, mint a particionálási érték. Aztán, hacsak a két bal és jobb mutató nem keresztezi egymást, kicseréljük a két elemet.

Minden iterációban egyenlő elemeket mozgatunk partitioningValue a két vége felé, és növelje a megfelelő számlálót:

while (true) {while (input [left] partitioningValue) {if (right == begin) break; jobb--; } if (balra == jobbra && input [balra] == particionálási érték) {csere (bevitel, kezdet + balEqualKeysCount, balra); leftEqualKeysCount ++; balra ++; } if (balra = = jobbra) {törés; } csere (bemenet, bal, jobb); if (input [left] == ​​partitioningValue) {swap (input, begin + leftEqualKeysCount, left); leftEqualKeysCount ++; } if (input [right] == ​​partitioningValue) {csere (input, right, end - rightEqualKeysCount); rightEqualKeysCount ++; } balra ++; jobb--; }

A következő szakaszban meg kell mozgassa az összes egyenlő elemet a középső két végből. Miután kiléptünk a ciklusból, a bal mutató egy olyan elemnél lesz, amelynek értéke nem kisebb, mint partitioningValue. Ezt a tényt felhasználva egyenlő elemeket kezdünk el mozgatni a két végétől a középpont felé:

jobb = bal - 1; for (int k = begin; k = begin + leftEqualKeysCount) csere (input, k, jobb); } for (int k = end; k> end - rightEqualKeysCount; k--, left ++) {if (left <= end - rightEqualKeysCount) csere (input, left, k); } 

Az utolsó szakaszban visszaadhatjuk a középső partíció határait:

visszatér az új partícióhoz (jobb + 1, bal - 1);

Végül vessünk egy pillantást megvalósításunk bemutatására egy minta bemeneten

6. Algoritmuselemzés

Általánosságban elmondható, hogy a Quicksort algoritmus átlagos esete az O (n * log (n)) és a legrosszabb esetben az O (n2) idő komplexitása. A duplikált kulcsok nagy sűrűségével szinte mindig a legrosszabb teljesítményt érjük el a Quicksort triviális megvalósításával.

Ha azonban a Quicksort háromirányú particionálási változatát használjuk, például a DNF particionálást vagy a Bentley particionálását, akkor képesek vagyunk megakadályozni a duplikált kulcsok negatív hatásait. Továbbá, a duplikált kulcsok sűrűségének növekedésével az algoritmusunk teljesítménye is javul. Ennek eredményeként akkor kapjuk meg a legjobb teljesítményt, ha minden kulcs egyenlő, és egyetlen partíciót kapunk, amely lineáris időben tartalmazza az összes azonos kulcsot.

Mindazonáltal meg kell jegyeznünk, hogy lényegében általános költségeket adunk hozzá, amikor a triviális egycsuklós particionálásról háromirányú particionáló sémára váltunk.

A DNF alapú megközelítésnél a rezsi nem függ az ismételt billentyűk sűrűségétől. Tehát, ha a DNF particionálást egy tömbhöz használjuk, minden egyedi kulccsal, akkor gyenge teljesítményt fogunk elérni ahhoz a triviális megvalósításhoz képest, ahol optimálisan választjuk a forgatást.

De Bentley-McIlroy megközelítése okosan cselekszik, mivel az egyenlő kulcsok két szélső végéből való elmozdítása a számuktól függ. Ennek eredményeként, ha ezt az algoritmust minden egyedi kulccsal rendelkező tömbhöz használjuk, akkor is meglehetősen jó teljesítményt fogunk elérni.

Összefoglalva: mind az egycsuklós, mind a háromirányú particionáló algoritmusok legrosszabb időbeli összetettsége O (nlog (n)). Azonban, a valódi előny a legjobb esetekben látható, ahol látjuk az idő bonyolultságát O (nlog (n)) egycsuklós particionáláshoz Tovább) háromirányú particionáláshoz.

7. Következtetés

Ebben az oktatóanyagban megismerkedtünk a Quicksort algoritmus triviális megvalósításával kapcsolatos teljesítményproblémákkal, amikor a bemenetnek sok ismételt eleme van.

A probléma kijavításának motivációjával mi különböző háromirányú particionálási sémákat tanult meg és hogyan tudjuk ezeket megvalósítani Java-ban.

Mint mindig, a cikkben használt Java-implementáció teljes forráskódja elérhető a GitHubon.