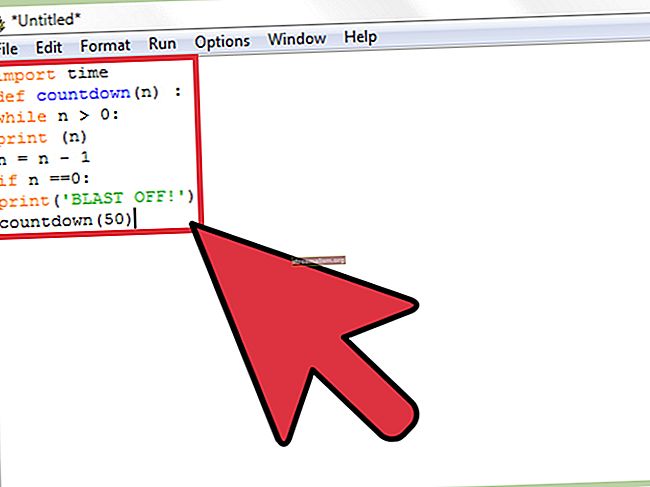
Útmutató a Java munkalopásához
1. Áttekintés
Ebben az oktatóanyagban megnézzük a munka lopás Java-koncepció.
2. Mit lop a munka?
A műrablást Java-ban vezették be azzal a céllal, hogy a szálak csökkentése a többszálas alkalmazásokban. Ez a fork / join keretrendszer segítségével történik.
2.1. Divide and Conquer Approach
A fork / join keretben a problémákat vagy feladatokat rekurzívan részfeladatokra bontják. A részfeladatokat ezután egyenként oldják meg, az aleredményeket egyesítve alkotják az eredményt:
Eredménymegoldás (Problémafeladat) {if (a probléma kicsi) közvetlenül megoldja a problémát más {a probléma felosztása független részekre, új részfeladatok elágazása az egyes részek megoldásához az egyes részek megoldásához csatlakozzon az összes részfeladathoz Kompozíció eredménye a részmegállapításokból}2.2. Munkásszálak
A lebontott feladatot a szálkészlet által biztosított munkásszálak segítségével oldják meg. Minden munkaszálnak lesznek olyan részfeladatai, amelyekért felelősek. Ezeket kettős végű várakozási sorokban (deques) tárolják.
Minden munkásszál úgy kapja meg a feladatait a deque-jéből, hogy folyamatosan leugor egy alfeladatot a deque tetejéről. Ha egy munkaszál deque-je üres, az azt jelenti, hogy az összes részfeladat kiugrott és befejeződött.
Ezen a ponton a munkásszál véletlenszerűen kiválaszt egy társ-szál-készlet szálat, amelytől „ellophatja” a munkát. Ezután az első be, az első kimenetel megközelítést (FIFO) használja az alfeladatok levételére az áldozat deque végének végétől.
3. Fork / Join Framework implementáció
A vagy használatával létrehozhatunk egy műlopó szálkészletet ForkJoinPool osztály vagy a Végrehajtók osztály:
ForkJoinPool commonPool = ForkJoinPool.commonPool (); ExecutorService workStealingPool = Executors.newWorkStealingPool ();A Végrehajtók osztály túlterhelt newWorkStealingPool metódus, amely egész argumentumot vesz fel a a párhuzamosság szintje.
Végrehajtók.newWorkStealingPool absztrakciója ForkJoinPool.commonPool. Az egyetlen különbség az Végrehajtók.newWorkStealingPool létrehoz egy készletet aszinkron módban és ForkJoinPool.commonPool nem.
4. Szinkron vs aszinkron szálkészletek
ForkJoinPool.commonPool a last-in, first-out (LIFO) sor konfigurációt használja, míg Végrehajtók.newWorkStealingPool first-in, first-out megközelítést (FIFO) használ.
Doug Lea szerint a FIFO megközelítésnek ezek az előnyei vannak a LIFO-val szemben:
- Csökkenti a vitát azáltal, hogy a lopók a tulajdonosként a deque másik oldalán működnek
- Kihasználja a rekurzív osztás és meghódítás algoritmusainak tulajdonságát a „nagy” feladatok korai generálásához
A fenti második pont azt jelenti, hogy egy régebbi ellopott feladatot tovább lehet bontani egy szál segítségével, amely ellopta.
A Java dokumentációjának megfelelően asyncMode nak nek igaz alkalmas lehet olyan esemény stílusú feladatokhoz, amelyekhez soha nem csatlakoznak.
5. Működő példa - Prímszámok keresése
Használjuk a példát arra, hogy a prímszámokat egy számgyűjteményből keressük a a munka-lopási keret számítási időbeli előnyei. Megmutatjuk a szinkron és az aszinkron szálkészletek használata közötti különbségeket is.
5.1. A prímszámok problémája
A prímszámok megtalálása a számok gyűjteményéből számítási szempontból költséges folyamat lehet. Ennek oka elsősorban a számgyűjtemény nagysága.
A Prímszámok osztály segít megtalálni a prímszámokat:
public class PrimeNumbers kiterjeszti a RecursiveAction {private int lowerBound; privát int felsőKötve; magán int részletesség; statikus végső lista GRANULARITIES = Arrays.asList (1, 10, 100, 1000, 10000); privát AtomicInteger noOfPrimeNumbers; PrimeNumbers (int lowerBound, int upperBound, int granularity, AtomicInteger noOfPrimeNumbers) {this.lowerBound = alsóBound; this.upperBound = felsőBound; ez.granularitás = szemcsésség; this.noOfPrimeNumbers = noOfPrimeNumbers; } // egyéb konstruktorok és módszerek private List subTasks () {List subTasks = new ArrayList (); mert (int i = 1; i <= ez a felsőkötés / szemcsésség; i ++) {int felső = i * szemcsésség; int alsó = (felső - szemcsésség) + 1; subTasks.add (új PrimeNumbers (alsó, felső, noOfPrimeNumbers)); } return alfeladatok; } @Orride védett void számítás () {if (((felsőBound + 1) - alsóBound)> részletesség) {ForkJoinTask.invokeAll (subTasks ()); } else {findPrimeNumbers (); }} void findPrimeNumbers () {for (int num = lowerBound; num <= upperBound; num ++) {if (isPrime (num)) {noOfPrimeNumbers.getAndIncrement (); }}} public int noOfPrimeNumbers () {return noOfPrimeNumbers.intValue (); }}Néhány fontos tudnivaló erről az óráról:
- Kiterjed RecursiveAction, amely lehetővé teszi számunkra a kiszámít módszer a feladatok kiszámításához egy szálkészlet segítségével
- Rekurzívan a feladatokat részfeladatokra bontja a részletesség érték
- A kivitelezők vállalják Alsó és felső kötött értékek, amelyek vezérlik azt a számtartományt, amelynek prímszámokat akarunk meghatározni
- Lehetővé teszi számunkra a prímszámok meghatározását akár műlopási szálkészlet, akár egyetlen szál segítségével
5.2. A probléma gyorsabb megoldása szálkészletekkel
Határozzuk meg a prímszámokat egyszálú módon és a munka ellopására szolgáló szálkészleteket is felhasználva.
Először nézzük meg a egyszálú megközelítés:
PrimeNumbers prímszámok = new PrimeNumbers (10000); primes.findPrimeNumbers ();És most, a ForkJoinPool.commonPool megközelítés:
PrimeNumbers prímszámok = new PrimeNumbers (10000); ForkJoinPool pool = ForkJoinPool.commonPool (); pool.invoke (prímek); pool.shutdown ();Végül megnézzük a Végrehajtók.newWorkStealingPool megközelítés:
PrimeNumbers prímszámok = new PrimeNumbers (10000); int párhuzamosság = ForkJoinPool.getCommonPoolParallelism (); ForkJoinPool stealer = (ForkJoinPool) Végrehajtók.newWorkStealingPool (párhuzamosság); lopó.invoke (prímek); lopó.leállítás ();Használjuk a hivatkozni módszere ForkJoinPool osztály feladatait adja át a szálkészletnek. Ez a módszer a RecursiveAction. A Java Microbench Harness használatával összehasonlítjuk ezeket a különböző megközelítéseket a műveletenkénti átlagos idő tekintetében:
# Futtatás kész. Összes idő: 00:04:50 Benchmark Mode Cnt ponthiba egységek PrimeNumbersUnitTest.Benchmarker.commonPoolBenchmark avgt 20 119.885 ± 9.917 ms / op PrimeNumbersUnitTest.Benchmarker.newWorkStealingPoolBenchmark avgt 20 119.791 ± 7.811 ms / op PrimeNumbersUnitest ms / opVilágos, hogy mindkettő ForkJoinPool.commonPool és Végrehajtók.newWorkStealingPool lehetővé teszi számunkra, hogy gyorsabban meghatározzuk a prímszámokat, mint egyszálú megközelítéssel.
A fork / join pool keretrendszer lehetővé teszi a feladat részfeladatokra bontását. Bontottuk a 10 000 egész szám gyűjteményét 1-100, 101-200, 201-300 és így tovább. Ezután meghatároztuk az egyes kötegek prímszámait, és elérhetővé tettük a prímszámok teljes számát noOfPrimeNumbers módszer.
5.3. Számítógépes munka lopása
Szinkron szálkészlettel, ForkJoinPool.commonPool addig helyezi a szálakat a készletbe, amíg a feladat még folyamatban van.Ennek eredményeként a munka lopásának szintje nem függ a feladat részletességének szintjétől.
Az aszinkron Végrehajtók.newWorkStealingPooljobban irányított, lehetővé téve a lopás munkájának szintjét a feladat részletességének szintjétől.
A lopással végzett munka szintjét a getStealCount a ForkJoinPool osztály:
hosszú lopások = forkJoinPool.getStealCount ();A munkalopási szám meghatározása Végrehajtók.newWorkStealingPool és ForkJoinPool.commonPool hasonló viselkedést kölcsönöz nekünk:
Executors.newWorkStealingPool -> Részletesség: [1], Lopások: [6564] Részletesség: [10], Lopások: [572] Részletesség: [100], Lopások: [56] Részletesség: [1000], Lopások: [60] Részletesség : [10000], lopások: [1] ForkJoinPool.commonPool -> Granularitás: [1], Steals: [6923] Granularitás: [10], Lopások: [7540] Granularitás: [100], Lopások: [7605] Granularitás: [1000], lopások: [7681] részletesség: [10000], lopások: [7681]Amikor a részletesség finomról durvára változik (1-10 000) mert Végrehajtók.newWorkStealingPool, a lopási munka szintje csökken. Ezért a lopások száma egy, ha a feladat nincs lebontva (10 000 részletesség).
A ForkJoinPool.commonPool más a viselkedése. A munka lopásának szintje mindig magas, és a feladat részletességének változása nem befolyásolja sokat.
Technikailag elmondható, hogy a prímszámokra példa az esemény stílusú feladatok aszinkron feldolgozását támogatja. Ennek az az oka, hogy megvalósításunk nem kényszeríti az eredmények összekapcsolását.
Eset lehet erre Végrehajtók.newWorkStealingPool az erőforrások legjobb felhasználását kínálja a probléma megoldásában.
6. Következtetés
Ebben a cikkben megvizsgáltuk a munkalopást és annak alkalmazását a fork / join keretrendszer segítségével. Megvizsgáltuk a munka lopásának példáit és azt is, hogy ez hogyan javíthatja a feldolgozási időt és az erőforrások felhasználását.
Mint mindig, a példa teljes forráskódja elérhető a GitHubon.