streamalism.org

1. Áttekintés

Ebben az oktatóanyagban feltárjuk a mélység-első keresést a Java-ban.

A mélység-első keresés (DFS) egy bejárási algoritmus, amelyet mind a Tree, mind a Graph adatstruktúrákhoz használnak. A mélység először a keresés az egyes ágak mélyére esik, mielőtt áttérne egy másik ág felfedezésére.

A következő szakaszokban először egy fa, majd egy grafikon megvalósítását vesszük szemügyre.

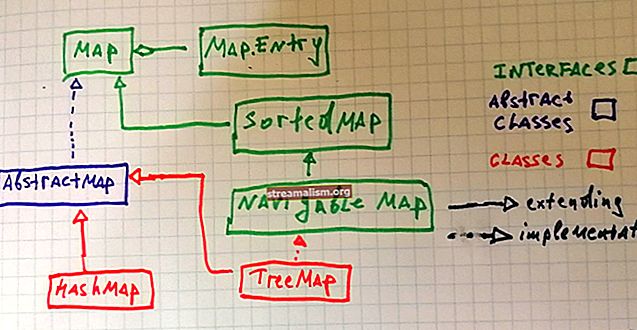
Ha meg szeretné tudni, hogyan lehet ezeket a struktúrákat Java-ban megvalósítani, tekintse meg a Bináris fa és grafikon korábbi oktatóanyagainkat.

2. Fa mélység-első keresés

Három különböző sorrend van egy fa áthaladásához DFS használatával:

1. Az előrendelés bejárása
2. Inorder Traversal
3. Postorder Traversal

2.1. Az előrendelés bejárása

Az előrendelés során először a gyökeret, majd a bal és a jobb részfát keresztezzük.

Egyszerűen rekurzió segítségével hajtsa végre az előrendelés bejárását:

• Látogatás jelenlegi csomópont
• Áthalad bal alfa
• Áthalad jobb alfa

public void traversePreOrder (Csomópont csomópont) {if (csomópont! = null) {látogatás (csomópont.érték); traversePreOrder (node.balra); traversePreOrder (csomópont.jobb); }}

Rekurzió nélkül is megvalósíthatjuk az előrendelés bejárását.

Az iteratív előrendeléses áthaladás megvalósításához szükségünk lesz egy Kazal, és elvégezzük ezeket a lépéseket:

• Nyom gyökér a mi stapadás
• Míg Kazal nem üres
  • Pop jelenlegi csomópont
  • Látogatás jelenlegi csomópont
  • Nyom jobb akkor gyermek bal gyermeknek Kazal

public void traversePreOrderWithoutRecursion () {Verem verem = új Verem (); Csomópont áram = gyökér; verem.push (gyökér); while (! stack.isEmpty ()) {current = stack.pop (); látogatás (aktuális.érték); if (current.right! = null) {stack.push (current.right); } if (current.left! = null) {stack.push (current.left); }}}

2.2. Inorder Traversal

A határon belüli bejáráshoz, először a bal alfát, majd a gyökeret, majd végül a jobb alfát járjuk át.

A bináris keresőfa belső áthaladása azt jelenti, hogy a csomópontokat értékeik növekvő sorrendjében haladjuk át.

A rekurzió segítségével egyszerűen megvalósíthatjuk az inorder bejárást:

public void traverseInOrder (Csomópont csomópont) {if (csomópont! = null) {traverseInOrder (csomópont.balra); látogatás (node.value); traverseInOrder (node.right); }}

Azt is megtehetjük rekurzió nélkül hajtsa végre az inorder bejárást, is:

• Nyom gyökér csomópont stapadás
• Miközben stapadás nem üres
  • Nyomjad bal gyermek rá Kazal, amíg el nem érünk jelenlegi csomópont bal oldali gyermeke
  • Látogatás jelenlegi csomópont
  • Nyom jobb gyermek rá Kazal

public void traverseInOrderWithoutRecursion () {Verem verem = új Verem (); Csomópont áram = gyökér; verem.push (gyökér); while (! stack.isEmpty ()) {while (current.balra! = null) {current = current.balra; verem.push (aktuális); } current = stack.pop (); látogatás (aktuális.érték); if (current.right! = null) {current = current.right; verem.push (aktuális); }}}

2.3. Postorder Traversal

Végül postai utakon a gyökér bejárása előtt bejárjuk a bal és a jobb részfát.

Követhetjük az előzőnket rekurzív megoldás:

public void traversePostOrder (Node node) {if (csomópont! = null) {traversePostOrder (node.left); traversePostOrder (csomópont.jobb); látogatás (node.value); }}

Vagy mi is rekurzió nélkül hajtsa végre a postorder utat:

• Nyom gyökér csomópont be stapadás
• Miközben stapadás nem üres
  • Ellenőrizze, hogy átmentünk-e már a bal és a jobb részfán
  • Ha nem, akkor nyomja meg jobb gyermek és bal gyermek rá Kazal

public void traversePostOrderWithoutRecursion () {Stack stack = new Stack (); Csomópont prev = gyökér; Csomópont áram = gyökér; verem.push (gyökér); while (! stack.isEmpty ()) {current = verem.peek (); logikai hasChild = (current.balra! = null || current.right! = null); logikai isPrevLastChild = (előző == current.right || (prev == current.lft && current.right == null)); if (! hasChild || isPrevLastChild) {current = verem.pop (); látogatás (aktuális.érték); prev = áram; } else {if (current.right! = null) {stack.push (current.right); } if (current.left! = null) {stack.push (current.left); }}}}

3. Grafikon Mélység-első keresés

A grafikonok és a fák közötti fő különbség az a grafikonok ciklusokat tartalmazhatnak.

Tehát a ciklusokban történő keresés elkerülése érdekében minden csomópontot megjelölünk, amikor meglátogatjuk őket.

A DFS gráfnak két megvalósítását látjuk, rekurzióval és rekurzió nélkül.

3.1. Grafikon DFS rekurzióval

Először kezdjük a rekurzióval:

• Egy adott csomópontból indulunk ki
• Mark jelenlegi csomópont meglátogatott
• Látogatás jelenlegi csomópont
• Keresse meg a meg nem látogatott szomszédos csúcsokat

public void dfs (int start) {logikai [] isVisited = új logikai [adjVertices.size ()]; dfsRecursive (start, isVisited); } private void dfsRecursive (int current, boolean [] isVisited) {isVisited [current] = true; látogatás (aktuális); mert (int dest: adjVertices.get (current)) {if (! isVisited [dest]) dfsRecursive (dest, isVisited); }}

3.2. Grafikon DFS rekurzió nélkül

Rekurzió nélkül is megvalósíthatjuk a grafikus DFS-t. Egyszerűen használjuk a Kazal:

• Egy adott csomópontból indulunk ki
• Nyom Rajt csomópont Kazal
• Míg Kazal nem üres
  • Mark jelenlegi csomópont meglátogatott
  • Látogatás jelenlegi csomópont
  • Nyomja meg a meg nem látogatott szomszédos csúcsokat

public void dfsWithoutRecursion (int start) {Verem verem = új Verem (); logikai [] isVisited = új logikai [adjVertices.size ()]; stack.push (start); while (! stack.isEmpty ()) {int current = verem.pop (); isVisited [current] = true; látogatás (aktuális); mert (int dest: adjVertices.get (aktuális)) {if (! isVisited [dest]) stack.push (dest); }}}

3.4. Topológiai rendezés

Nagyon sok alkalmazás van a gráfmélység-első keresésre. A DFS egyik leghíresebb alkalmazása a Topological Sort.

Az irányított gráf topológiai rendezése a csúcsainak lineáris elrendezése, így minden forrásnál a forráscsomópont a cél elé kerül.

A topológiai rendezéshez szükségünk lesz egy egyszerű kiegészítésre az imént megvalósított DFS-hez:

• A meglátogatott csúcsokat veremben kell tartanunk, mert a topológiai rendezés a meglátogatott csúcsokat fordított sorrendben jelenti
• Csak akkor tologatjuk a meglátogatott csomópontot a veremhez, miután minden szomszédját bejártuk

public List topologicalSort (int start) {LinkedList eredmény = új LinkedList (); logikai [] isVisited = új logikai [adjVertices.size ()]; topologicalSortRecursive (start, isVisited, eredmény); visszatérési eredmény; } private void topologicalSortRecursive (int current, logikai [] isVisited, LinkedList result) {isVisited [current] = true; mert (int dest: adjVertices.get (aktuális)) {if (! isVisited [dest]) topológiaiSortRecursive (dest, isVisited, eredmény); } eredmény.addFirst (aktuális); }

4. Következtetés

Ebben a cikkben megvitattuk a fa és a grafikon adatszerkezeteinek mélységbeli keresését.

A teljes forráskód elérhető a GitHub oldalon.