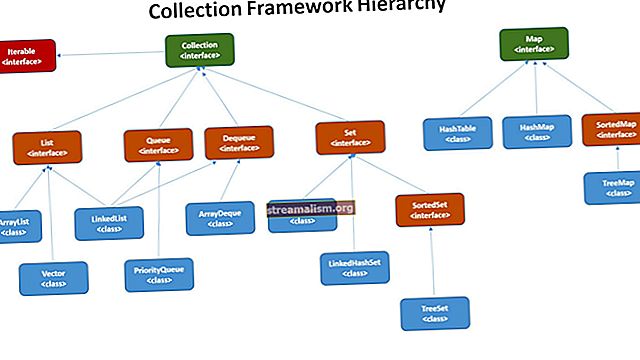
Bevezetés a zár nélküli adatstruktúrákba Java példákkal
1. Bemutatkozás
Ebben az oktatóanyagban megtudhatjuk, hogy melyek a nem blokkoló adatstruktúrák, és miért fontos alternatívája a zároláson alapuló egyidejű adatstruktúráknak.
Először áttekintünk néhány kifejezést, például akadálymentes, zármentes, és várakozás nélküli.
Másodszor megvizsgáljuk a nem blokkoló algoritmusok alapvető építőelemeit, mint például CAS (összehasonlítás és cserélés).
Harmadszor, megvizsgáljuk a zár nélküli sor bevezetését a Java-ban, és végül felvázoljuk azt a megközelítést, hogyan lehet elérni várakozási szabadság.
2. Zár versus éhezés
Először nézzük meg a különbség a blokkolt és az éhező szál között.

A fenti képen a 2. szál zárat szerez az adatszerkezeten. Amikor az 1. szál megkísérli megszerezni a zárat, akkor meg kell várnia, amíg a 2. szál felszabadítja a zárat; nem megy tovább, mielőtt megszerezné a zárat. Ha felfüggesztjük a 2. szálat, miközben a zárat tartja, akkor az 1. szálnak örökké várnia kell.
A következő kép a szál éhezést szemlélteti:

Itt a 2. szál hozzáfér az adatstruktúrához, de nem szerez zárat. Az 1. szál egyszerre próbál hozzáférni az adatszerkezethez, észleli az egyidejű hozzáférést, és azonnal visszatér, tájékoztatva a szálat, hogy nem tudja befejezni (piros) a műveletet. Az 1. szál ezt követően próbálja újra, amíg a műveletet nem sikerül végrehajtani (zöld).
Ennek a megközelítésnek az az előnye, hogy nincs szükségünk zárra. Az azonban megtörténhet, hogy ha a 2. szál (vagy más szálak) nagy frekvenciával férnek hozzá az adatstruktúrához, akkor az 1. szálnak nagyszámú próbálkozásra van szüksége, amíg végül sikerrel jár. Éhezésnek hívjuk.
Később meglátjuk, hogy a összehasonlítás és cserélés művelettel elérjük a nem blokkoló hozzáférést.
3. A nem blokkoló adatstruktúrák típusai
A nem blokkoló adatstruktúrák három szintjét különböztethetjük meg.
3.1. Akadálymentes
Az akadálymentesség a nem blokkoló adatstruktúra leggyengébb formája. Itt csak egy szál folytatására van szükség, ha az összes többi szál fel van függesztve.
Pontosabban: egy szál nem éhezik tovább, ha az összes többi szál fel van függesztve. Ez abban különbözik a zárak ilyen értelemben való használatától, hogy ha a menet zárra várt, és a zárat tartó szál fel van függesztve, akkor a várakozó szál örökké várna.
3.2. Zármentes
Az adatstruktúra biztosítja a zárolás szabadságát, ha bármikor folytatható legalább egy szál. Az összes többi szál éhezhet. Az akadály-szabadság különbsége, hogy van legalább egy nem éhező szál, még akkor is, ha nincsenek felfüggesztve.
3.3. Várakozás-mentes
Az adatszerkezet várakozásmentes, ha zárolatlan, és minden szál véges számú lépés után garantáltan folytatódik, vagyis a szálak nem fognak éhen halni „indokolatlanul sok” lépésnél.
3.4. Összegzés
Összefoglaljuk ezeket a definíciókat grafikus ábrázolásban:

A kép első része akadálymentességet mutat, mivel az 1. szál (felső szál) folytatódhat (zöld nyíl), amint felfüggesztjük a többi szálat (alul sárga színnel).
A középső rész zár-szabadságot mutat. Legalább az 1. szál előrehaladhat, míg mások éhezhetnek (piros nyíl).
Az utolsó rész a várakozási szabadságot mutatja. Itt garantáljuk, hogy az 1. szál folytatódhat (zöld nyíl) egy bizonyos éhezési periódus után (piros nyilak).
4. Nem blokkoló primitívek
Ebben a szakaszban három olyan alapvető műveletet vizsgálunk meg, amelyek segítenek abban, hogy az adatstruktúrákon lezárás nélküli műveleteket építsünk ki.
4.1. Hasonlítsa össze és cserélje ki
A reteszelés elkerülése érdekében az egyik alapvető művelet a összehasonlítás és cserélés (CAS) művelet.
Az összehasonlítás és cserélés ötlete az, hogy egy változó csak akkor frissül, ha még mindig ugyanaz az értéke, mint annak idején, amikor a változó értékét lekértük a fő memóriából. A CAS atomi művelet, ami azt jelenti, hogy a letöltés és a frissítés együtt egyetlen művelet:

Itt mindkét szál lekéri a 3. értéket a fő memóriából. A 2. szál sikeres (zöld), és a változót 8-ra frissíti. Mivel az 1. szálon az első CAS arra számít, hogy az érték még 3 lesz, a CAS nem működik (piros). Ezért az 1. szál ismét beolvassa az értéket, és a második CAS sikeres lesz.
A legfontosabb itt az, hogy a CAS nem szerez zárat az adatszerkezeten, hanem visszatér igaz ha a frissítés sikeres volt, különben visszatér hamis.
A következő kódrészlet vázolja a CAS működését:
volatilis int érték; logikai értékű cas (int várható érték, int új érték) {if (érték == várható érték) {érték = új érték; return true; } return false; }Csak akkor frissítjük az értéket az új értékkel, ha még mindig megvan a várt értéke, ellenkező esetben visszatér hamis. A következő kódrészlet bemutatja, hogyan hívható a CAS:
void testCas () {int v = érték; int x = v + 1; while (! cas (v, x)) {v = érték; x = v + 1; }}Megpróbáljuk frissíteni az értékünket, amíg a CAS művelet sikeres lesz, vagyis vissza nem tér igaz.
Lehetséges azonban, hogy egy szál elakad az éhezésben. Ez akkor fordulhat elő, ha más szálak ugyanabban a változóban végeznek CAS-t egyidejűleg, így a művelet egy adott szálon soha nem fog sikeres lenni (vagy ésszerűtlenül sok időt vesz igénybe a siker). Mégis, ha a összehasonlítás és cserélés kudarcot vall, tudjuk, hogy egy másik szál sikeres volt, így biztosítjuk a globális haladást is, amire a zár-szabadsághoz szükség van.
Fontos megjegyezni, hogy a hardvernek támogatnia kell összehasonlítás és cserélés, hogy ez valóban atomi művelet legyen reteszelés nélkül.
A Java biztosítja a összehasonlítás és cserélés az osztályban sun.misc.biztonságos. Azonban a legtöbb esetben nem ezt az osztályt kell közvetlenül használnunk, hanem Atomic változókat.
Továbbá, összehasonlítás és cserélés nem akadályozza meg az A-B-A problémát. Ezt a következő szakaszban vizsgáljuk meg.
4.2. Load-Link / Store-Conditional
A összehasonlítás és cserélés van load-link / store-conditional. Először nézzük meg újra összehasonlítás és cserélés. Mint korábban láthattuk, a CAS csak akkor frissíti az értéket, ha a fő memóriában szereplő érték továbbra is az az érték, amelyre számítunk.
A CAS azonban akkor is sikeres, ha az érték megváltozott, és időközben visszaállt a korábbi értékére.
Az alábbi kép ezt a helyzetet szemlélteti:

Mind az 1. szál, mind a 2. szál beolvassa a változó értékét, ami 3. Ezután a 2. szál végrehajt egy CAS-t, amely sikeresen beállítja a változót 8-ra. Ezután ismét a 2. szál hajt végre egy CAS-t a változó visszaállítására 3-ra, ami szintén sikerrel jár. Végül az 1. szál elvégez egy CAS-ot, várva a 3. értéket, és sikerrel is jár, annak ellenére, hogy változónk értéke kétszer módosult.
Ezt nevezzük A-B-A problémának. Ez a viselkedés természetesen nem okozhat problémát a használati esettől függően. Másoknak azonban nem biztos, hogy kívánatos. A Java biztosítja a load-link / store-conditional a ... val AtomicStampedReference osztály.
4.3. Letöltés és hozzáadás
Egy másik alternatíva az letöltés és hozzáadás. Ez a művelet egy adott értékkel növeli a fő memória változóját. Ismét az a fontos szempont, hogy a művelet atomszerűen történik, ami azt jelenti, hogy más szál nem zavarhatja.
A Java biztosítja a letöltés és hozzáadás atomi osztályaiban. Ilyenek például AtomicInteger.incrementAndGet (), amely növeli az értéket és visszaadja az új értéket; és AtomicInteger.getAndIncrement (), amely visszaadja a régi értéket, majd növeli az értéket.
5. Hozzáférés egy összekapcsolt sorhoz több szálból
Annak érdekében, hogy jobban megértsük, hogy két (vagy több) szál egyszerre fér hozzá a sorhoz, nézzünk meg egy összekapcsolt sort és két szálat, amelyek megpróbálnak egyidejűleg hozzáadni egy elemet.
A várakozási sor egy duplán összekapcsolt FIFO-sor, ahol az utolsó elem (L) és a változó után új elemeket adunk hozzá farok rámutat arra az utolsó elemre:

Új elem hozzáadásához a szálaknak három lépést kell végrehajtaniuk: 1) hozzák létre az új elemeket (N és M), a következő elemre mutató mutatóval nulla; 2) legyen hivatkozás az előző elemre L-re, az L-pont következő elemére pedig N-re (M, ill. 3) Van farok mutasson N-re (M, ill. M):

Mi romolhat el, ha a két szál egyszerre hajtja végre ezeket a lépéseket? Ha a fenti kép lépései az ABCD vagy ACBD, L, valamint a sorrendben hajtódnak végre farok, M.-re mutat. N továbbra sem lesz összekapcsolva a várólistával.
Ha a lépéseket az ACDB sorrendben hajtjuk végre, farok N-re, míg L M-re fog mutatni, ami következetlenséget okoz a sorban:

Természetesen a probléma megoldásának egyik módja az, hogy egy szál zárat szerez a sorban. Az a megoldás, amelyet a következő fejezetben nézünk meg, egy zármentes művelet segítségével oldja meg a problémát a korábban látott CAS művelet segítségével.
6. Nem blokkoló várólista a Java-ban
Nézzünk meg egy alapvető zár nélküli sort a Java-ban. Először nézzük meg az osztály tagjait és a kivitelezőt:
public class NonBlockingQueue {private final AtomicReference fej, farok; privát végleges AtomicInteger méret; public NonBlockingQueue () {head = new AtomicReference (null); tail = új AtomicReference (null); méret = új AtomicInteger (); méret.készlet (0); }} A fontos rész a fej és farok hivatkozások deklarálása AtomicReferences, amely biztosítja, hogy ezekre a hivatkozásokra vonatkozó bármilyen frissítés atomi művelet legyen. Ez a Java-adattípus végrehajtja a szükségeset összehasonlítás és cserélés művelet.
Ezután nézzük meg a Node osztály megvalósítását:
private class Csomópont {private volatile T value; privát illékony Csomópont következő; private volatile Csomópont előző; public Node (T érték) {this.value = érték; this.next = null; } // szerelők és beállítók}Itt fontos az deklarálni az előző és a következő csomópontra történő hivatkozásokat illó. Ez biztosítja, hogy ezeket a hivatkozásokat mindig a fő memóriában frissítsük (így közvetlenül láthatók az összes szál számára). Ugyanez a tényleges csomópontértéknél.
6.1. Zármentes hozzá
Zár nélküli hozzá A művelet biztosítja, hogy az új elemet hozzáadjuk a farokhoz, és hogy nem szakad le a sorról, még akkor sem, ha több szál egyidejűleg szeretne új elemet hozzáadni:
public void add (T elem) {if (elem == null) {dobjon új NullPointerException (); } Csomópont csomópont = új Csomópont (elem); Csomópont currentTail; do {currentTail = tail.get (); node.setPrevious (currentTail); } while (! tail.compareAndSet (currentTail, csomópont)); if (csomópont.elõzõ! = null) {csomópont.elõzõ.következõ = csomópont; } head.compareAndSet (null, csomópont); // az első elem méretének beszúrásához.incrementAndGet (); }A figyelem elengedhetetlen része a kiemelt vonal. Megpróbáljuk felvenni az új csomópontot a sorba, amíg a CAS műveletnek nem sikerül frissítenie a farokot, amelynek továbbra is ugyanazon faroknak kell lennie, amelyhez az új csomópontot csatoltuk.
6.2. Zármentes kap
Az add-művelethez hasonlóan a lock-free get-művelet biztosítja, hogy visszaadjuk az utolsó elemet, és a farokot az aktuális helyzetbe mozgatjuk:
public T get () {if (head.get () == null) {dobjon új NoSuchElementException (); } Csomópont currentHead; Node nextNode; do {currentHead = fej.get (); nextNode = currentHead.getNext (); } while (! head.compareAndSet (currentHead, nextNode)); size.decrementAndGet (); return currentHead.getValue (); }Ismételten a legfontosabb rész, amire figyelni kell, a kiemelt vonal. A CAS művelet biztosítja, hogy az aktuális fejet csak akkor mozgassuk, ha közben más csomópontot nem távolítottunk el.
A Java már biztosítja a nem blokkoló várólista, a ConcurrentLinkedQueue. Ez a cikkben leírt M. Michael és L. Scott zár nélküli sorának megvalósítása. Érdekes megjegyzés itt, hogy a Java dokumentáció azt állítja, hogy ez a várakozás nélküli sor, ahol valójában zármentes. A Java 8 dokumentáció helyesen hívja meg a megvalósítást zármentes.
7. Várakozás nélküli várólisták
Mint láttuk, a fenti megvalósítás az zármentesazonban nem várakozás nélküli. A míg hurkok mind a hozzá és kap A módszer hosszú ideig (vagy bár valószínűtlen, de örökké) hurokba szállhat, ha sok szál fér hozzá a sorunkhoz.
Hogyan érhetjük el a várakozási szabadságot? A várakozás nélküli algoritmusok megvalósítása általában meglehetősen bonyolult. Az érdeklődő olvasót erre a cikkre irányítjuk, amely részletesen leírja a várakozás nélküli várólistát. Ebben a cikkben nézzük meg annak az alapgondolatát, hogy miként lehet megközelíteni a várakozás nélküli várólista megvalósítását.
A várakozás nélküli várólista megköveteli, hogy minden szál garantáltan haladjon (véges számú lépés után). Más szavakkal, a míg az add and get metódusok hurkjainak bizonyos számú lépés után sikeresnek kell lenniük.
Ennek elérése érdekében minden szálhoz hozzárendelünk egy segítő szálat. Ha az a segítőszál sikeresen hozzáad egy elemet a várólistához, az segít a másik szálnak beilleszteni az elemét, mielőtt egy másik elemet beillesztene.
Mivel a segítő szálnak van egy segítője, és a szálak teljes listáján minden szálnak van segítője, garantálhatjuk, hogy egy szál sikeresen beilleszthető legyen, miután minden szál elvégzett egy beszúrást. A következő ábra szemlélteti az ötletet:

Természetesen a dolgok bonyolultabbá válnak, amikor dinamikusan hozzáadhatunk vagy eltávolíthatunk szálakat.
8. Következtetés
Ebben a cikkben a nem blokkoló adatstruktúrák alapjait láthattuk. Elmagyaráztuk a különböző szinteket és az alapvető műveleteket összehasonlítás és cserélés.
Ezután megvizsgáltuk az a zármentes sor Java-ban. Végül felvázoltuk a megvalósítás gondolatát várakozási szabadság.
A cikk összes példájának teljes forráskódja elérhető a GitHub oldalon.